| Idioma : |
|
| Comunitat enciclopèdia |Enciclopèdia Respostes |Enviar pregunta |Coneixement de vocabulari |Pujar coneixement |
Circumvolució |
 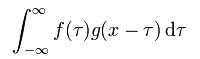  |
|
Definicions Tecnologia Nom xinès: convolució Nom Anglès: convolució Definició: funcions matemàtiques sobre dos tipus de càlcul infinit. Per a la funció f1 (t) i f2 (t), la convolució s'expressa com: on: "" per als símbols d'operació de convolució.La ciència aplicada: electricitat (un subjecte); Teoria General (dos subjectes) El contingut d'amunt pel Consell Nacional de Ciència i Tecnologia va anunciar el Comitè d'Aprovació En l'anàlisi funcional, convolució, la convolució o la convolució (Anglès: Convolució) a través de les dues funcions f i g genera una funció matemàtica del tercer operador, després de la caracterització de la funció f i g de la tapa i de la traducció La superposició acumulatius. Si els participants com una funció de indicador d'intervals de la funció de convolució, la convolució també poden ser considerats com la promoció de "mitjana mòbil". Connotació bàsica Convolució és un breu anàlisi d'un important operacions matemàtiques. Deixeu que: f (x), g (x) és integrable en R1 dues funcions per a la integració (a la dreta): Es pot provar en gairebé tots els nombres reals x, existeix la integral. Per tant, amb diferents valors de x, la integral en la definició d'una nova funció h (x), f i g es diu la funció de convolució, denotat per h (x) = (f * g) (x). Fàcil de verificar, (f * g) (x) = (g * f) (x), i (f * g) (x) segueix sent funció integrable. Això significa que en lloc de la multiplicació de convolució, L1 (R1) 1 és un espai algebraica, o fins i tot àlgebra de Banach. Convolució i la transformada de Fourier té una estreta relació. Prenent una mica de propietat que les dues funcions són iguals per al producte de la transformada de Fourier de la convolució de la transformada de Fourier, l'anàlisi de Fourier admet molts problemes es poden simplificar. Funció obtingut per la convolució f * g f i g són generalment millors que suau. Especialment quan g és una funció suau amb conjunt compacte, f és localment integrable, la seva convolució f * g és una funció suau. L'avantatge d'aquest tipus, per a qualsevol funció f integrable, vostè pot simplement construir una aproximació de funcions sense problemes a la columna f fs, aquest mètode s'anomena una funció de suavitzat o regularització. El concepte de convolució es pot estendre també a la sèrie, així com funcions generalitzades a l'altura. Definició La funció f i g s'anomena convolució, que és una de les funcions després de la panoràmica amb tapa i la integració del producte de l'altra funció és una funció de la quantitat d'accés a la paella. Interval d'integració depèn del domini de f i g. Convolució de les funcions f i g es pot definir com: z (t) = f (t) * g (t) = ∫ f (m) g (tm) dm. Per a la definició d'una funció en el domini discret, convolució es defineix com (F * g) [m] = Σf (n) g (m-n) Algorisme de convolució ràpida Quan es tracta d'una longitud finita N, N ^ 2 vegades a sobre les operacions. Amb una mica d'algorisme ràpid es pot reduir la complexitat en O (nlogn). L'algorisme més comú de convolució ràpida per convolució circular utilitzant la transformada ràpida de Fourier. També es poden incloure per un altre enfocament no-FFT, es mostra amb en la conversió. Multi funció de convolució D'acord amb la, definició integral flip, pa, també pot definir diverses funcions en una integral similar: Naturalesa Diversos operador convolució satisfà les següents propietats: Commutativa llei distributiva associativa de la multiplicació on A és una combinació de qualsevol nombre real (o complexa). Teorema diferencial on Df denota un f-diferencial, si es refereix a un operador diferencial discret domini, incloent la diferència cap endavant i cap enrere diferència són dues: Diferència Forward: diferència de versions anteriors: Teorema de convolució |
| Usuari Revisió |
|
Sense comentaris encara |